Spatio-temporal picture in the Gurevich model
Assumptions:
- All runaway electrons move with the same speed υ along the z-axis against a uniform electric field.
- Avalanches of runaway electrons are localized strictly inside the cell.
- The cell width is much larger than the runaway electron avalanche width.
Let an avalanche of runaway electrons be generated at the point {z_0} at the time {t_0}. Then its space-time distribution will be as follows:
| {f_{RREA}(z, t, z_0, t_0) = e^{\nu (t — t_0)} \delta\left( (z — z_0) — \upsilon(t — t_0) \right) S(z) S(L — z)} |
Where {\nu = \frac{\lambda_ {RREA}}{\upsilon}} is the reproduction rate of runaway electrons, {\delta} is the Dirac delta function, {S} is the Heaviside step function, L — cell length.
Let a source of seed electrons be located at the point {z_0}, which generates {N} electrons per unit time along the {z} axis against the electric field.
Then, at the point {z} at time {t}, there will be the following number of runaway electrons:
| {F(z, t, z_0) = N e^{\frac{\nu}{\upsilon}(z — z_0)} S\left(\frac{z — z_0}{\upsilon}\right) S\left(t — \frac{z — z_0}{\upsilon}\right)} |
Suppose that seed electrons are generated uniformly along the cell. Then, at the point {z}, {N} electrons are produced per unit time. It should be noted that {N} here differs from the previous {N} in dimension.
In the case under consideration, at the point {z} at time {t} there will be the following number of runaway electrons:
| {F(z, t) = N \lambda_{RREA} S(L — z) S(z) \left} |
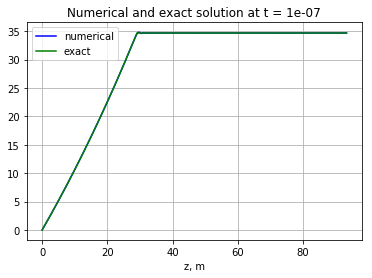
For the space-time distribution in the latter case, the following equation was also numerically solved:
| {\frac{\partial F}{\partial z} + \frac{1}{\upsilon}\frac{\partial F}{\partial t} = \frac{1}{\lambda_{RREA}} F + N(t,z)} |
- {F(t, z)} is the number of runaway electrons.
- {N(t, z)} — source function.
- {\upsilon} — runaway electron velocity.
- {\nu_f = \frac {\upsilon} {\lambda_ {RREA}}} is the multiplication frequency of runaway electrons.
The numerical solution coincided with the analytical one, and its result is shown in the figure:
A criterion for infinite positron feedback in Relativistic Feedback Discharge Model
Terrestrial Gamma-ray Flashes (TGF) — short (~ 100 μs) and intense flashes of terrestrial gamma radiation, the source of which is thunderstorms. This remarkable natural phenomenon has been observed for over 20 years from satellites (for example, Fermi), as well as ground-based observatories (for example, the Array telescope).It is believed that the source of gamma radiation is avalanches of runaway electrons accelerated by thunderstorm electric fields.
Joseph Dwyer proposed a model of runaway electron avalanches — the Relativistic Feedback Discharge Model (RFDM). According to Dwyer, there is a feedback mechanism in the dynamics of avalanches, which leads to the reproduction of avalanches and, therefore, their endless existence. Such an amazing process is caused by the creation of positrons by the bremsstrahlung of electron avalanches.
In this work, an analytical study of RFDM is carried out. The spatial distributions of particles were obtained for all generations of self-replicating avalanches. And also a criterion for the existence of positron infinite feedback in thunderclouds is derived. The results are confirmed by simulation on Geant4.
The criterion can be formulated as follows. In a cell with a uniform critical electric field, the process of infinite multiplication of runaway electron avalanches due to positron feedback is possible if the following inequality is satisfied:
| {\Gamma = \frac{P \lambda_{RREA} \lambda_{-}}{(\lambda_- + \lambda_{RREA}) \lambda_2 \lambda_{\gamma} \lambda_{\gamma \rightarrow e^-e^+} cos\alpha} \left(\frac{\lambda_{RREA} \lambda_{x}}{\lambda_{x} — \lambda_{RREA}}\right)^2 \left( e^{\frac{L(\lambda_{x} — \lambda_{RREA})}{\lambda_x\lambda_{RREA}}} — 1 — \frac{L(\lambda_{x} — \lambda_{RREA})}{\lambda_x\lambda_{RREA}} \right) > 1} |
- {P = P_{e^+ reversal} \cdot P_{e^- reversal}} — the total probability of reversals (product, since the reversal of the electron and the reversal of the positron, are independent). A reversal is a reversal + runaway.
- {\lambda_{RREA}} — the length of the exponential rise of RREA.
- {\lambda_{x}} — is the path length of the positron before annihilation. Also, this number effectively takes into account the acceleration of the positron.
- {\lambda_{\gamma}} — is the path length of a runaway electron before the production of a gamma quantum with energy sufficient for the production of an electron-positron pair.
- {\lambda_{\gamma \rightarrow e^+e^-}} — is the mean free path of gamma before the birth of a positron (electron-positron pair).
- {\alpha} — the average angle relative to the z-axis, at which the gamma is flying.
- {\lambda_{2}} — is the path length of the positron before the birth of the runaway electron.
- {L} — cell length.
- {\lambda_{-}} — the length of exponential decay of gamma-ray flux.
From the criterion, the conditions for the occurrence of TGF in the Dwyer model are obtained. They are shown in the figure: